Solution Method for Kepler's Equation
From ANCS Wiki
The goal for the solution of Kepler's equation is to determine the eccentric anomaly accurately, given the mean anomaly and eccentricity.
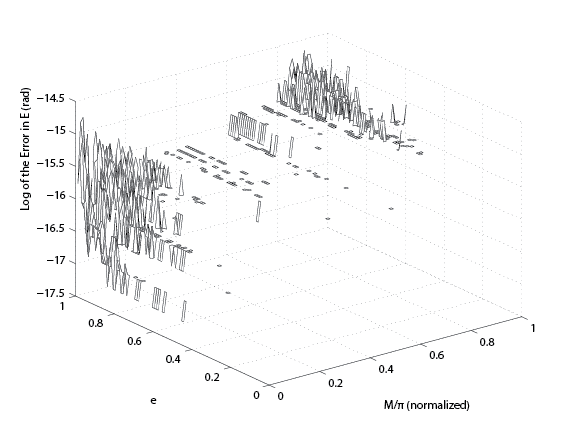
This study presents a new approach to solve this very well-documented problem. We focus on demonstrating the procedure for both the elliptical and hyperbolic cases. It is found that by means of a series approximation, an angle identity, the application of Sturm's theorem and an iterative correction method, the need to evaluate transcendental functions or store tables is eliminated. A 15th-order polynomial is developed through a series approximation of Kepler's equation. Sturm's theorem is used to prove that only one real roots exists for this polynomial for the given range of mean anomaly and eccentricity. An initial approximation for this root is found using a 3rd-order polynomial. Then a one time generalized Newton-Raphson correction is applied to obtain accuracies to the level of around 10-15 rad for the elliptical case and 10-13 rad for the hyperbolic case, which is near machine precision.
Results from this study can be found at:
[1] Pimienta-Penalver, A., and Crassidis, J. "Accurate Kepler Equation Solver without Transcendental Function Evaluations." AAS Jer-Nan Juang Astrodynamics Symposium. College Station, TX, June 2012, AAS Paper #2012-612