Covariance Intersection: Difference between revisions
From ANCS Wiki
No edit summary |
No edit summary |
||
| Line 18: | Line 18: | ||
==Covariance Intersection== | ==Covariance Intersection== | ||
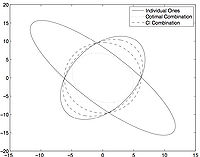
[[File:Ciexample.jpg|thumbnail|right|200px|Alt=SSA|Covariance Intersection]] An elegant solution for the fusion of estimates with unknown correlations is the Covariance Intersection (CI) algorithm [Julier and Uhlmann, 1997]. As the name suggests, the CI algorithm is routed in the fiundamentals of Gaussian intersection. Appreciation for the CI algorithm is gained by considering the fusion of two estimates in 2D. In 2D the covariance of a Gaussian random variable can be interpreted as an ellipse. If multiple estimates of the same 2D state vector are available, their covariance ellipses will intersect as shown. The CI algorithm expresses the covariance of the fused estimate as the smallest covariance ellipse which contains all of the intersection of the two individual covariances. Depending on the confidence in each estimate or a desired final statistic, each individual covariance can be weighted by a scalar value which leads the CI algorithm to include a family of solutions as shown. | [[File:Ciexample.jpg|thumbnail|right|200px|Alt=SSA|Covariance Intersection]] An elegant solution for the fusion of estimates with unknown correlations is the Covariance Intersection (CI) algorithm [Julier and Uhlmann, 1997]. As the name suggests, the CI algorithm is routed in the fiundamentals of Gaussian intersection. Appreciation for the CI algorithm is gained by considering the fusion of two estimates in 2D. In 2D the covariance of a Gaussian random variable can be interpreted as an ellipse. If multiple estimates of the same 2D state vector are available, their covariance ellipses will intersect as shown. The CI algorithm expresses the covariance of the fused estimate as the smallest covariance ellipse which contains all of the intersection of the two individual covariances. Depending on the confidence in each estimate or a desired final statistic, each individual covariance can be weighted by a scalar value which leads the CI algorithm to include a family of solutions as shown. | ||
Another elegant property of the CI algorithm is that, while being derived from a geometric viewpoint, it can also be derived from a matrix- and scalar-weighted optimization problem. This property allows the CI algorithm to be extended to the fusion of higher dimensional state vectors and an arbitrary number of estimates. | |||
==Covariance Intersection for Attitude Estimation== | |||
While the CI algorithm provides a meaningful and elegant solution for the problem of fusion under unknown correlations, the fusion of attitude states is not trivial. The main difficulty with fusing attitude estimates is the choice of attitude parametrization. The traditional attitude parametrization of choice for space applications, the quaternion, must satisfy a unit norm constraint. This leads the CI fused estimate to be the solution of a constrained optimization problem. For state vectors including only a single quaternion there are several solutions to the resulting optimization problem. | |||
==References== | |||
Andrle, M.S., and Crassidis, J.L., “[http://ancs.eng.buffalo.edu/pdf/ancs_papers/2012/geom_int.pdf Geometric Integration of Quaternions],” AIAA/AAS Astrodynamics Specialist Conference, Minneapolis, MN, Aug. 2012, AIAA Paper #2012-4421. | |||
Revision as of 20:47, 26 November 2012
Decentralized Systems
Systems comprised of a number of computing nodes all supporting a common mission. All nodes can be given the same task or asked to support the mission through a subset of tasks. Decentalized systems offer several advantages over their centralized counterparts including:
- Each node does not require intrinsic knowledge of the system topology
- Topology is variable. Nodes can be added or subtracted without significantly impacting the overall system
- Less vulnerable to single-point failures
- Computational load can be spread amongst nodes for efficiency
Decentralized systems also suffer from some disadvantages:
- All nodes may not have access to all information contained within the system
- Multiple nodes have access to the same information
Examples of decentralized systems include robotic swarms, cooperative UAVs, formation flying spacecraft and formation of synthetic apertures using multiple smaller sensors.
Decentralized Estimation
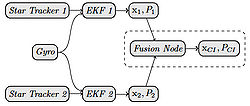
Decentralized estimation representes an important aspect of decentralized systems. Because various nodes within the system may not have access to all measurements within the system, the individual estimates will be suboptimal. In a perfect world there would exist a means to combine the estimates from all of the nodes into a single estimate which makes use of all system measurements and is optimal. Difficulty arises because some measurements may be used by more than one node leading the estimates from those nodes to be correlated. An example of such a system is the spacecraft attitude estimator shown. Because each extended Kalman filter (EKF) makes use of a common gyro measurement the two estimates will be correlated. The problem to be solved is how can we efficiently and consistently fuse the individual estimates from each EKF to obtain the best possible estimate?
Covariance Intersection
An elegant solution for the fusion of estimates with unknown correlations is the Covariance Intersection (CI) algorithm [Julier and Uhlmann, 1997]. As the name suggests, the CI algorithm is routed in the fiundamentals of Gaussian intersection. Appreciation for the CI algorithm is gained by considering the fusion of two estimates in 2D. In 2D the covariance of a Gaussian random variable can be interpreted as an ellipse. If multiple estimates of the same 2D state vector are available, their covariance ellipses will intersect as shown. The CI algorithm expresses the covariance of the fused estimate as the smallest covariance ellipse which contains all of the intersection of the two individual covariances. Depending on the confidence in each estimate or a desired final statistic, each individual covariance can be weighted by a scalar value which leads the CI algorithm to include a family of solutions as shown.
Another elegant property of the CI algorithm is that, while being derived from a geometric viewpoint, it can also be derived from a matrix- and scalar-weighted optimization problem. This property allows the CI algorithm to be extended to the fusion of higher dimensional state vectors and an arbitrary number of estimates.
Covariance Intersection for Attitude Estimation
While the CI algorithm provides a meaningful and elegant solution for the problem of fusion under unknown correlations, the fusion of attitude states is not trivial. The main difficulty with fusing attitude estimates is the choice of attitude parametrization. The traditional attitude parametrization of choice for space applications, the quaternion, must satisfy a unit norm constraint. This leads the CI fused estimate to be the solution of a constrained optimization problem. For state vectors including only a single quaternion there are several solutions to the resulting optimization problem.
References
Andrle, M.S., and Crassidis, J.L., “Geometric Integration of Quaternions,” AIAA/AAS Astrodynamics Specialist Conference, Minneapolis, MN, Aug. 2012, AIAA Paper #2012-4421.